Gabriel's Horn

Üblicherweise, wenn man sich eine Körper mit unendlicher großer Oberfläche vorstellt, denkt man auch, dass das Volumen unendlich sein müsste.

Aber der Körper, bennant nach dem Horn das der Erzengle Gabriel spielt, hat genau diese Eigenschaft.

Um den Körper zu konstruieren nimmt man die Funktion für und rotiert sie um die x Achse.


Die Erklärung von Rezo so bezog sich dabei auf die diskrete Variante von diesem Paradox, auch genannt Gabriel's Wedding Cake. Diskret im gegensatz zu Analytisch beudeutet etwas vereinfacht in der Mathematik, dass wir nicht mit Rellen Zahlen arbeiten, sonder nur mit Ganzen Zahlen oder auch Brüchen.

Enssprechend ist die Funktion, die um die x-Achse rotiert wird, bei dem "Kuchen" ( beudeutet abrunden).


Da hier die Mathematik deutlich einfacher ist schauen wir uns auch wider den "Kuchen" an. Zunächst die Bildliche Vorstellung:

Stellen wir uns einen Kuchen mit dem Volumen vor. Halbiert man diesen, hat jede Hälft nun . Jetzt halbiert man eine Hälft wieder und legt davon die Hälft wieder auf die andere Hälft.
Damit hat man eine 2er Stapel mit und das Viertel.

Dies macht man nun einfach Unendlich oft :D Dabei wächst die Fläche des Stapels jedes man, wenn man ein neues Stück darauf legt, also ins Unendliche. Aber das Volumen vom Kuchen wird nie aufgebraucht, da ja immer halbiert wird.

Aber schauen wir uns das mal Mathematisch an:

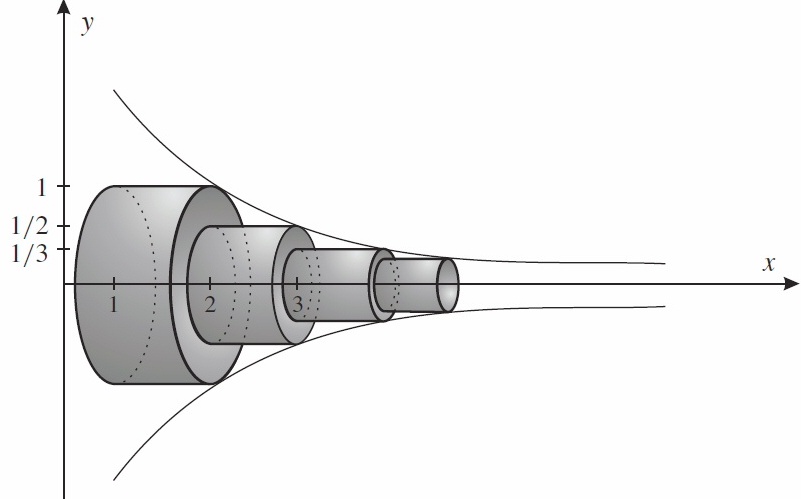
Rotiert man also die Funktion um die x-Achse, erhält man einen Unendlich langen Stapel an Zylindern (wie rechts zu sehen). Um davon das Volumen zu berechen, berechen wir also das Volumen von jedem Zylinder und nehmen davon die Summe. Aus der Grundschule wissen wir, das Volumen eins Zylider wird mit

berechnet.

Der Radius von unseren Zylindern ist das Abstand von der x-Achse. Also für den -ten Zylinder ist der Radius . Höhe ist hier für jeden Zylinder , was man am Grpahen erkennen kann oder daran, oder genauer wenn man betrachtet, sieht man, das die funktion genau für ein Intervall von gleich bleibt und dann springt.

Jetzt müssen wir mit einer Summe alle unendliche viele Zylinder zusammen addieren:

Diese Summe lässt sich vereinfachen, indem wir das aus der Summe holen und das quadrat in den Bruch rein holen

Dank Euler wissen wir, dass die Reihe gegen konvergiert (Basler Problem).

Also ist das endliche Volumen all userer Zylinder ("Kuchenteile") insgesammt

Schauen wir uns jetzt die Oberfläche all diese Zylinder an:

Zur Vereinfachung schauen wir uns auch nur die Mantelfläche der Zylinder, also nicht die Flächen oben und unten. Denn, wenn die Mantelfäche schon unedlich ist, sind die Grundflächen auch nicht mehr relevant. Aus der Grundschule kennen wir die Formel für die Mantelfläche eines Zylinders

Das wäre also hier für den -ten Zylinder .

Dann wieder als Summe für alle Zylinder

Die Reihe ist die sogenannte Harmonische Reihe, von der bekannt ist, dass sie divergiert, also gegen Unendlich läuft.

Somit ist die Fläche alle Zylinder Unendlich groß.

Jetzt in stetig

Die Mathematik hinter Gabriels Horn ist noch etwas kompliziert, wird aber in diesem Video ganz gut erläuter

Quellen

Edit on GitHub!