Hilberts Hotel
Motivation
Hilbers Hotel ist ein Sinnbild, eine Metapher, um das Konzpet der Unendlichkeit zu verstehen. Dahinter liegen kontrekte Mathmathische Überlegungen.
Mathematiker teilen Zahlen in bestimmte Mengen ein:
Alle Zahlen die keine Kommastelle haben heißen Ganze Zahlen:
Alle Ganzen Zahlen die positv sind heißen Natürliche Zahlen:
Alle Zahlen die sich als Bruch schreiben lassen heißen Rationale Zahlen:
Jetzt die wichtige Frage: Welche dieser Mengen ist Größer?
Ohne ein gutes Konzept von Unendlichkeit würde man denken, die Ganzen Zahlen müssten doch zumindest größer als die Natürlichen Zahlen sein, schließliche enthalten die Ganzen Zahlen ja die Natürlichen Zahlen und noch die negativen Zahlen dazu. Jetzt steigen wir mit Hilberts ein.
David Hilbert
David Hilbert war einer deutscher Mathematiker. Nicht nur löste Hilbert selber viele Mathematische Probleme, er war auch sehr aktiv in der Lehre stelle auch 1900 in Paris "Hilbert's Problems" vor. Diesen waren noch ungelöste mathematische Grundsatzfragen, die zu den wichtigsten Mathemaischen erkentinissen unserer Zeit führen. Zum Beispiel Gödels Unvollständikeits Satz war eine Antwort auf Problem Nr. 2.

David Hilbert
Rezo erwähnte noch, dass Hilber vor Einstein die Allgemeine Relativitätstheorie veröffenticht haben soll. Das stimmt so halb. Einsteil und Hilbert haben 1915 in Göttingen Zusammengearbeitet und auch Vorlesungen gegeben. Dann hat Einstein die Gravitationsgleichungen veröffentlicht, eine Elementarer Baustein der Allgemeinen Relativitätstheorie (aber das soll mal lieber ein/e Physiker*in erklären). Hilbert veröffentlichte Zeigleich ähnliche Formel aber nutzte sie noch weiter (Einstein-Hilbert). Hilbert gab aber Einstein full credit für seine Arbeit.
Hilbers Hotel
Man stelle sich ein Hotel vor mit unendlichen vielen Zimmer, die alle Besetzt sind. Das Hotel ist also voll. Das hört sich zunächst mal sehr krude an, aber erstens ist es nur ein Modell und zweitens ist das often in der Mathemathik so: Man definiert sich erstmal ein Szenario und schaut dann, was darus folgt. Wir definieren hier ein Hotel mit undendliche vielen Zimmern.

Noch ein Zimmer frei?
Kommt jetzt noch ein Gast und möchte noch ein Zimmer, ist die Antwort erstmal nein. Denn egal zu welchem der unendliche vielen Zimmern man geht, alle sind voll.
Aber der Hotel Manager ist schlau und sagt jedem Gast, er soll ein Zimmer weiter gehen. Also Zimmer 1 geht in Zimmer 2, Zimmer 2 geht in Zimmer 3 usw. Allgmeint:
Zimmer
Dann ist Zimmer 1 frei. Dort kann der neue Gast dann einziehen. Hmm, obwhol wir jetzt schon unendliche viele Gäste hatten. Haben wir jetzt mehr?

Noch unendliche Zimmer frei?
Jetzt kommt eine Ganze Buslandung mit Gästen an. In dem Bus sind unendliche viele Gäste. Wie bekomment wir die jetzt unter?
Naiv könnte man sagen, wir machen das, was wir bei einem Gast gemacht haben, einfach unendlich mal. Aber das funktioniert nicht, denn dann werden wir nie fertig. Wir haben nie alle untergebracht, weil immer min. einer im Bus wartet.
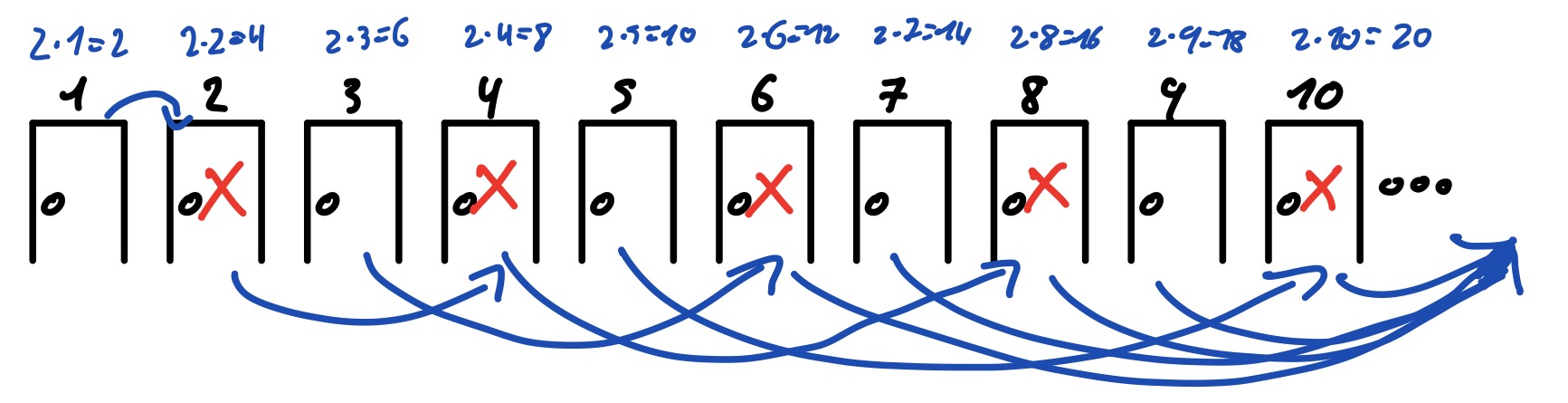
Dem Manager fällt was besseres ein: Er sagt jedem er soll eine Zimmernummer mal 2 nehmen in und das Zimmer gehen. Allgemein:
Zimmer
Da wenn man eine Zahl mal 2 nimmt, immer eine gerade Zahl herauskommt, sind jetzt unendliche viele Zimmer mit geraden Zimmer nummern besetzt, aber alle Zimmer mit einer ungeraden Zimmernummer sind frei. Da es wie man weiß unendliche viel ungerade Zahlen gibt, sind auch unendlich viel Zimmer frei und jeder aus dem Bus hat ein Zimmer, in das er gehen kann.
Noch unendliche mal unendliche viele Zimmer frei?
Als letzes kommen nun unendliche viele Busse am Hotel an, mit jeweils unendlich vielen Gästen. Um dieses Problem zu lösen gibt es jetzt mehrere Methoden.
Dafür legen wir zunächst ein paar varibeln fest. Wir geben jedem Buss eine Nummer und in jedem Bus nummerieren wir die Sitzplätze.
(Mathematisch genauer: man muss jetzt nur eine bijektive Pairing function
Primfaktoren
Für diesne Methode ist es wichtig zu wissen, dass jeden natürliche Zahl eine eindeutige Primfaktorzerlegung hat. Wir nehmen und also einfach die ersten beiden Primzahlen 2 und 3 und sagen:
Der Gast aus Bus
Somit ist kein Zimmer dopplet belegt, aber es werden einige Zimmer leer bleiben.
Der vorteil ist, dass wir das Spiel beliebig weiter spielen können. Sagen wir z.B. es kommen jetzt auf unendliche viele Straßen jeweils unendliche viele Busse mit jeweils unendlich viele Gästen an. Dann baruchen wir nur eine Primzahl mehr und weisen jedem Gast die Zimmernummer
Weitere Methoden
TODO
Hört bei Rezo im Podcast nach oder schaut auf der Wiki seite nach
Wieder zurück zur Ausgangsfrage
Die Antwort, welche der drei Mengen größer ist, lautet: die sind alle gleich Groß. Nämlich alle abzählbar unendlich.
Denn bei der Ausgangslage im Hotel, wo alle Zimmer besetzt sind, haben wir sozusagen die unendliche vielen Zimmer mit den Natürlichen Zahlen gefüllt. Denn es sind ja die Zimmer
Die Ganzen Zahlen werden dargesellt durch den ersten Bus, der hinzukommt. Denn die postiven Zahlen sind schon im Hotel, jetzt kommmen die unendlich vielen negativen Zahlen hinzu. Also passen auch die Ganzen Zahlen in das gleich große Hotel.
Die Rationalen Zahlen passen auch in das Hotel. Da Brüche ein Kombination aus 2 Unendlichen Mengen ist (Unendlich Möglichenkeiten auf und unter dem Bruchstrich, siehe Kartesisches Produkt), passen auch diese in Hilberts Hotel, mit unendlich vielen Zimmern.
Und jetzt das WOHA mit Cliffhänger
Obwohl wir gerade scheibar gezeigt haben, dass alle unendlichen Mengen gleich groß sind, auch wenn eine in der andren enthalten ist (
Es gibt verschieden große Unendlichekeiten, denn es gibt Mengen die nicht in Hilberts Hotel passen. Hierbei verweise ich aber an den nächstes Fact.
Weiteres
Hilber nutze dieses Modell in einer seiner Vorlesungen. Mehr historisches dazu hier. Es wird nun in vielen populärwissenschaftlich Veröffentlichungen.
Hier gibt es noch Videos, die das sehr gut Visualisieren: